Piano Synthesizer

The goal of this project is to create realistically sounding piano synthesizer; it should not use any prerecorded sound samples, but should be based on a mathematical and physical modelling as much as possible. At the same time, creating complete mathematical model is not a goal, so if there is a way to make it sound better based on the method that is not necessarily physical in its foundations, that is fine.

At this point I have an implementation that sound reasonably good, but it contains some code that can not be published as is. If from description below you feel like you understand what I'm talking about and can provide some help, please do so.

Sound samples

Sounds presented below were produced from a corresponding MIDI files. They represent direct model output without any post-processing. I don't own copyright for any of the MIDI files, they are the property of their respective authors.

Name	Files
J. S. Bach - Air	[midi, 23 kB] [mp3, 4.1 MB] [short mp3, 471.8 kB]
J. Brahms - Hungarian Dance No. 2	[midi, 39 kB] [mp3, 3.2 MB] [short mp3, 512.2 kB]
F. Chopin - Fantaisie Impromptu	[midi, 22 kB] [mp3, 4.4 MB] [short mp3, 608.2 kB]
W. A. Mozart - Fantasy in D minor (kv397)	[midi, 16 kB] [mp3, 5.1 MB] [short mp3, 555.9 kB]

If you have a MIDI file that you'd like to hear synthesized, ask me and I'll gladly do it.

Basic mathematical model

Piano sound exhibits very complex behavior and it is almost impossible to produce realistic piano sound based solely on the mathematical modelling. Presented model tries to replicate the result without starting from the basic mathematical and physical principles.

Piano note sound can be decomposed into set of partials. Here is a simple equation showing such decomposition:

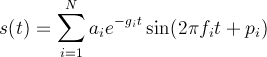
$s(t) = \sum_{i=1}^{N} a_i e^{-g_i t} \sin(2 \pi f_i t + p_i)$

Here a_i is an initial amplitude, g_i is a decay rate, f_i is a partial frequency and p_i is a phase.

Two of the most prominent characteristics of the piano sound are beating and two-stage decay. Those effects result in a fast decay of the amplitude after the strike and a slowly decaying aftersound. During the slow decay phase there is audible beating in the sound. Nature of those effects is not really known to the science, there are few viable theories described in the literature.

Equation above does not reproduce this behavior, so it can not produce realistic piano sound. One way of replicating beating and two-stage decay is replacing each partial by multiple independent sine waves:

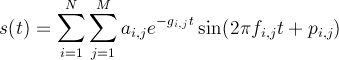
$s(t) = \sum_{i=1}^{N} \sum_{j=1}^{M} a_{i,j} e^{-g_{i,j} t} \sin(2 \pi f_{i,j} t + p_{i,j})$

In this equation M represents the number of strings per key for the current key (normally 2 in a low register and 3 in a high register). j=1 corresponds to the initial sound; j=2 and j=3 (if exists) correspond to the aftersound. Previous research shows that the initial fast decay in a piano note sound should be a measurably flatter than the aftersound. General relationship between parameters values is defined in a following way:

a_i,1 >> a_i,2; a_i,1 >> a_i,3; a_i,2 ≈ a_i,3
g_i,1 >> g_i,2; g_i,1 >> g_i,3; g_i,2 ≈ g_i,3
f_i,1 < f_i,2; f_i,1 < f_i,3; f_i,2 ≈ f_i,3
p_i,1 = p_i,2 = p_i,3

In this case difference between f_i,2 and f_i,3 is a beating frequency.

a_i,j, g_i,j, f_i,j and p_i,j will also depend on the key press dynamics. Adjustment for the press dynamics is done by modifying precalculated base values, so run-time computational complexity of this algorithm is very low.

Future work

Now I'm looking for a way to calculate parameters of the model based only on a physical values, like string length, piano body size, etc.

Less ambitious plan is to replace existing proprietary algorithm with an open source implementation and publish complete source code.